Reactive Nonholonomic Traj Gen
Reactive Nonholonomic Trajectory Generation via Parametric Optimal Control - - Alonzo Kelly, Bryan Nagy
Abstract
文章讨论了怎么实时生成一条轨迹,将轨迹问题建模成最优控制问题,进而转化为非线性优化问题。主要贡献在于 三阶曲率多项式 的公式推导及求解。
注:第二章介绍最优控制部分没看懂,对求解不影响,忽略;
【Keywords】Polynomial Spirals , Clothoids
Solution Using Polynomial Spirals
3.2 Clothoids
回旋曲线 定义其曲率为线性变化:
$$ \kappa (s) = a + bs$$
3.3 Polynomial Spirals
场景:已知起始点和终点的状态,求一条曲线
将曲率表示为 n 阶多项式,用以满足端点的约束条件;
3.4 Reduction to Decoupled Quadratures
多项式螺旋线可以通过封闭形式积分得到航向角 heading
$$ \begin{aligned} \kappa(s)&=a+bs+cs^2+ds^3 \newline \theta(s)&=\theta_0 + \int \kappa ds =\theta_0 + as+ \frac{bs^2}{2} + \frac{cs^3}{3}+ \frac{ds^4}{4} \end{aligned} \tag{1} $$
再对行程积分,[generalized Fresnel integrals 广义菲涅尔积分]
$$ \begin{aligned} x(s)&=x_0+\int_0^s cos \left[as+ \frac{bs^2}{2} + \frac{cs^3}{3}+ \frac{ds^4}{4} \right] ds\newline y(s)&=y_0+\int_0^s sin \left[as+ \frac{bs^2}{2} + \frac{cs^3}{3}+ \frac{ds^4}{4} \right] ds\newline \end{aligned} $$ 所以,位置无法以 closed-form 形式求解。
· 求解多项式
·· 获取 [a/b/c/d] 初值
··· 查表
参考: Basic_SD_Algorithm/Path_Generation
在起点处建立坐标系,保证起点坐标 $[0,0,0]$,在给定的圆弧内查找最近 伪终点,从而得到一条近似的初值。
··· 固定一个参数求解
参考:https://blog.csdn.net/github_39582118
根据 $(1)$ 式定义可得 $$ \begin{aligned} \kappa(0)&=p_0 =\kappa_0 ,<起点曲率>\newline \kappa(\frac{s_f}{3})&=p_1 =\kappa_0+\frac{b}{3}s_f+\frac{c}{9}{s_f}^2+\frac{d}{27}{s_f}^3 \newline \kappa(\frac{2s_f}{3})&=p_2 =\kappa_0+\frac{2b}{3}{s_f}+\frac{4c}{9}{s_f}^2+\frac{8d}{27}{s_f}^3 \newline \kappa(s_f)&=p_3 = \kappa_0+bs_f+c{s_f}^2+d{s_f}^3 \newline \end{aligned} \tag{2} $$ 借用 $Matlab$ 求解 $b, c, d$
% Ax = B
clear all
close all
clc
syms p0 p1 p2 p3 s qf
B = [p1-p0; p2-p0; p3-p0]
disp(' ')
A = [s/3 , (s/3)^2 , (s/3)^3 ;
2*s/3 , (2*s/3)^2 , (2*s/3)^3 ;
s , s^2 , s^3 ]
disp(' ')
disp('solve: ')
disp(' ')
fun = linsolve(A,B);
pretty(fun)
得到结果:
B =
p1 - p0
p2 - p0
p3 - p0
A =
[ s/3, s^2/9, s^3/27]
[ (2*s)/3, (4*s^2)/9, (8*s^3)/27]
[ s, s^2, s^3]
solve:
/ 11 p0 - 18 p1 + 9 p2 - 2 p3 \
| - --------------------------- | [b]
| 2 s |
| |
| (2 p0 - 5 p1 + 4 p2 - p3) 9 |
| --------------------------- | [c]
| 2 |
| 2 s |
| |
| (p0 - 3 p1 + 3 p2 - p3) 9 |
| - ------------------------- | [d]
| 3 |
\ 2 s /
令 $d=0$ ,同时根据 $(1)$ 式中末端角度,求解
theta = p0*s + fun(1)/2*s^2 + fun(2)/3*s^3;
disp(' ')
% pretty(theta)
p1_with_p2 = solve(theta==qf, p1);
p2_ans = solve(p0-3*p1_with_p2+3*p2-p3==0,p2); % d = 0
p1_ans = -(4*qf - 5*p0*s - 15*p2_ans*s + 4*p3*s)/(12*s);
b_ans = simplify(-(11*p0 - 18*p1_ans + 9*p2_ans - 2*p3)/(2*s));
c_ans = simplify((9*(2*p0 - 5*p1_ans + 4*p2_ans - p3))/(2*s^2));
disp(' ')
disp('solve b & c when set d=0')
pretty(b_ans)
pretty(c_ans)
得到 $b, c$ 的初值,其中 qf 表示 $\theta_f-\theta_0$ :
4 p0 s - 6 qf + 2 p3 s
- ---------------------- [b]
2
s
3 p0 s - 6 qf + 3 p3 s
---------------------- [c]
3
s
求取初值的过程中,仅使用了已知的角度和曲率,所以位置误差应该比较随机。
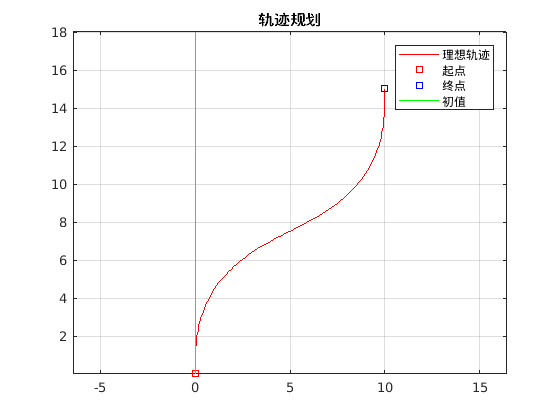
Other
因示例代码中牛顿迭代法收敛性不好,怀疑是初值或者非线性的影响。最终使用 Nelder Mead 方法收敛,所以这里不进行偏导的推导。
另外,目测查表的初值要好一些。