Home

Optimal Trajectory in a Frenet Frame

  • Optimal Trajectory Generation for Dynamic Street Scenarios in a Frenet Frame
  • Local Path Planning and Motion Control for AGV in Positioning

https://github.com/ChenBohan/Robotics-Path-Planning-04-Quintic-Polynomial-Solver.git

Summary

常见的轨迹规划算法，想要得到最优轨迹，通常都需要动态障碍物的精确模型。文章中提出的是一种基于采样的反应式轨迹生成算法。根据路宽、速度范围、预测时间范围采样得到 大量轨迹，删除不可行轨迹后，根据代价进行排序，选择 最优轨迹 执行。

【注】代码比论文好懂

frenet

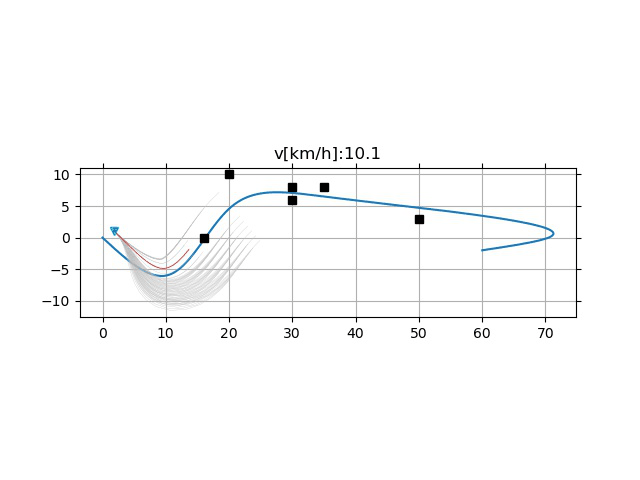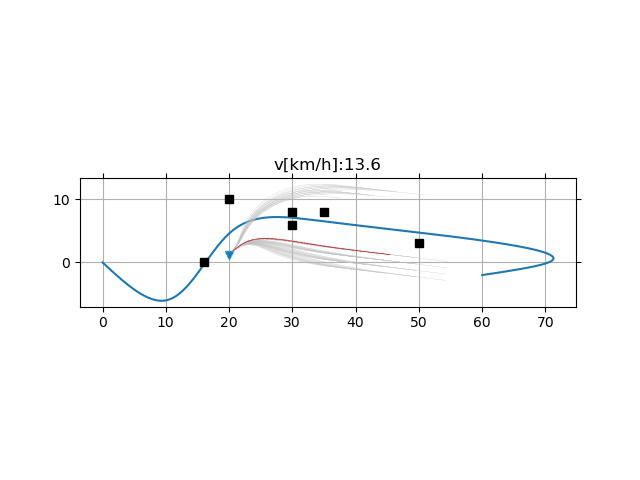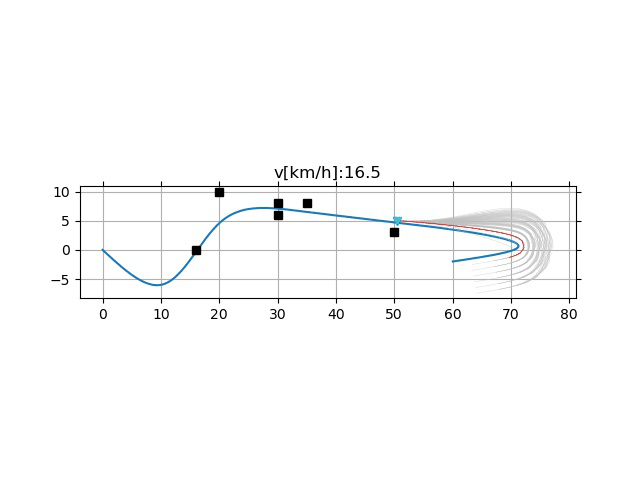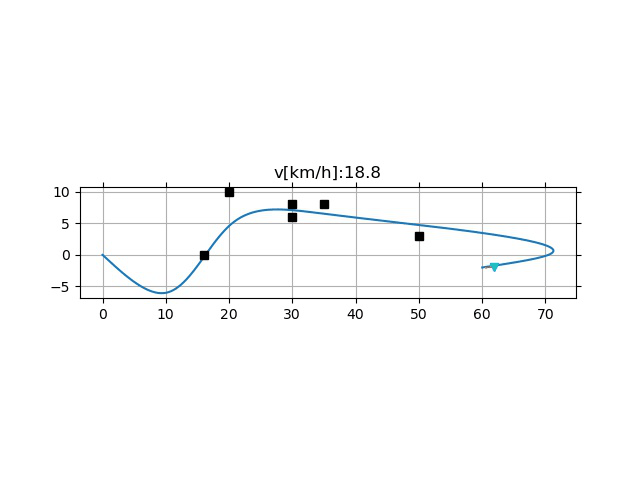
KeyPoints

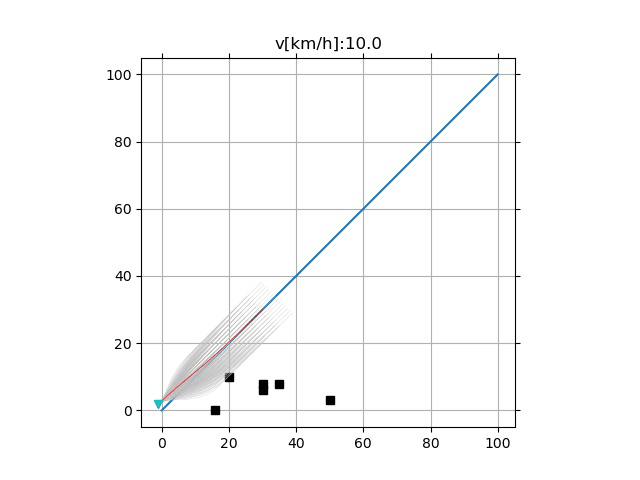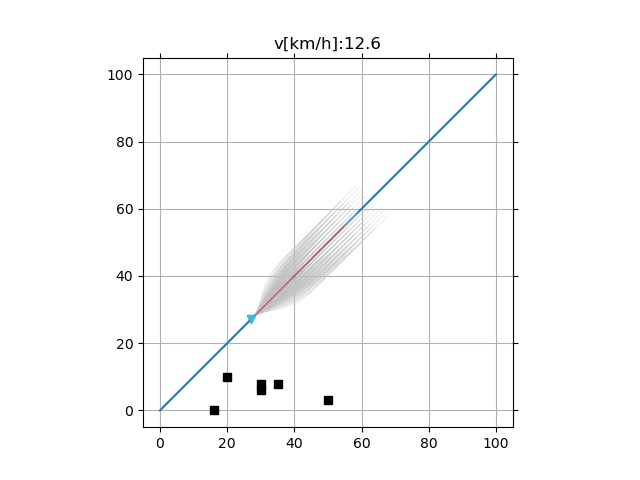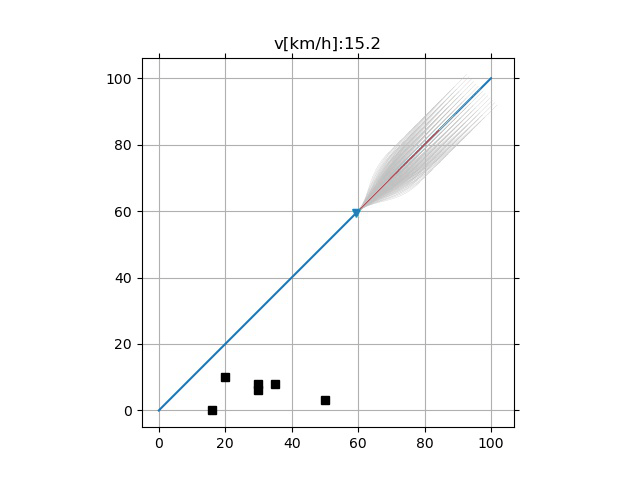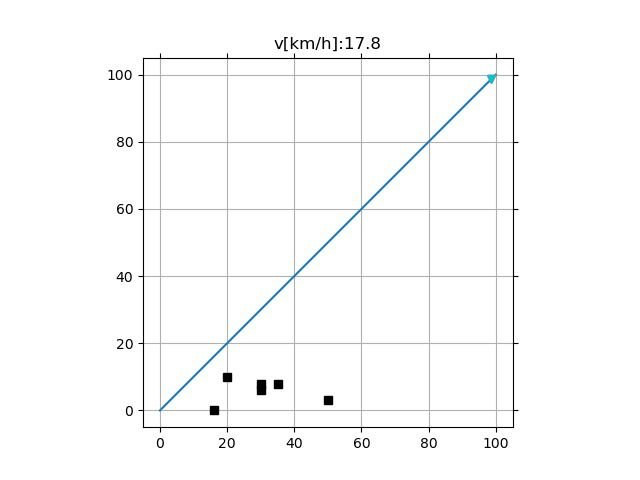
  • 采样频率的影响
    • 过低的采样频率可能引起超调（下）
frenet-overshoot

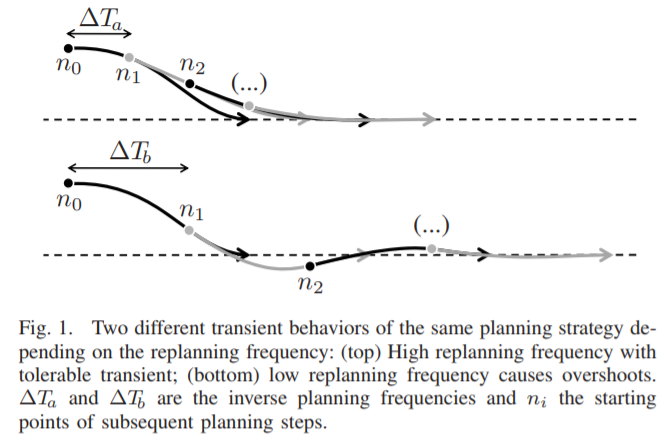
  • Frenet 坐标系

    对于轨迹上一点 reference，以 切线方向 $\vec{t}_r$ 和法线方向 $\vec{n}_x$ 建立坐标系；$d(t)$ 表示机器人偏离轨迹的距离，$s(t)$ 表示机器人行程。
    图中，$\vec{t}_x, \vec{n}_x$ 仅用于表示机器人在 Frenet 坐标系的位姿；

frenet-overshoot

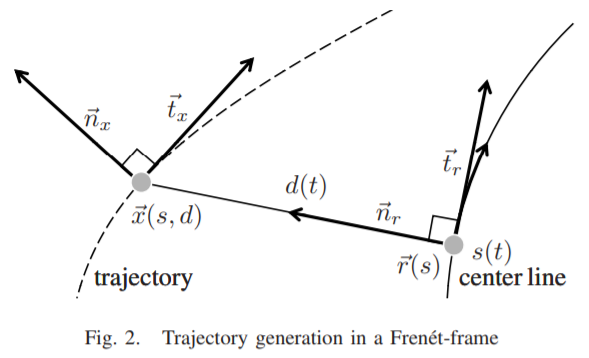
Frenet 流程

Lateral Movement

起始状态 $[d_0, \dot{d_0}, \ddot{d_0}]$，沿用上一状态，保证运动连续性； 目标状态要求 $\dot{d_1} = \ddot{d_1} = 0$，以保证最终的沿线运动，即，

$$[d_1, \dot{d_1}, \ddot{d_1}, T]_{ij} = [d_i, 0, 0, T_j]$$

对采样空间中的 $i, j$ 分别采样，得到 Frenet 坐标系的横向运动轨迹集。

Longitudinal Movement

起始状态 $[s_1, \dot{s_1}, \ddot{s_1}]$ ；

根据场景和当前状态，对不同的目标状态采样： $$[s_1, \dot{s_1}, \ddot{s_1}, T]_{ij} = [ [s_1(T_j)+\Delta s_i], \dot{s}_1(T_j), \ddot{s}_1(T_j), T_j ]$$

  • Follow 跟随前车
    • 根据交通规则和前车 [leader] 状态
  • Merging 汇入车流
    • 目标点在前、后两车的中间
  • Stopping 停车
    • $s_{target} = s_{stop}$
    • $\dot{s_t} = 0, \ddot{s_t} = 0$
  • Velocity Keeping 定速巡航
    • 只对速度、加速度约束求解
    • $[\dot{s_1}, \ddot{s_1}, T]_{ij} = [[\dot{s_d} + \Delta \dot{s_i}], 0, T_j]$

Combining Lateral & Longitudinal Trajectories

  • 对 $T_{lat}$ 和 $T_{lon}$ 分别检查加速度，需注意保留部分加速能力，保证控制裕度
    • 同时需要为 巡线 预留横向加速能力，因此需要保证目标轨迹的曲率上限；
  • 在笛卡尔坐标系，检查曲率是否超限，检查是否碰撞；
  • 不引入障碍物的启发代价，从而避免复杂的参数调整

Appendix I

Frenet coordinates -> Global coordinates

$$[s, \dot{s}, \ddot{s}; d, \dot{d}, \ddot{d}/d, d', d''] \mapsto [\vec{x}, \theta_x, \kappa_x, v_x, a_x]$$

其中，$\dot{d} = \frac{d}{dt}d$ ，$d' = \frac{d}{ds}d$

一通复杂的转换，两个坐标系之间主要通过机器人行程 $s$ 实现转换；所以，坐标转换是离散采样实现的。轨迹的非线性对转换精度影响比较大。

Appendix II

已知首尾状态，求解 四阶、五阶多项式

Quintic Polynomial

五次多项式 标准形式：

$$ s(t) = a_0 + a_1 t + a_2 t^2 + a_3 t^3 + a_4 t^4 + a_5 t^5$$

已知，起始状态 $ t=0$ 时的状态，即 $$ \begin{aligned} a_0 &= s_0 \newline a_1 &= \dot{s}_0 \newline a_2 &= \frac{\ddot{s}_0}{2} \newline \end{aligned} $$ 代入标准形式，得到终点 $t=T$ 的状态： $$ \begin{aligned} s_T &= s_0 + \dot{s_0}T + \frac{\ddot{s}_0}{2}T^2 + a_3 T^3 +a_4 T^4 +a_5 T^5 \newline \dot{s}_T &= \dot{s}_0 + \ddot{s}_0 T + 3 a_3 T^2 + 4 a_4 T^3 + 5 a_5 T^4\newline \ddot{s}_T &= \ddot{s}_0 + 5 a_3 T + 12 a_4 T^2 + 20 a_5 T^3 \newline \end{aligned} $$ 整理， $$ \begin{aligned} a_3 T^3 +a_4 T^4 +a_5 T^5 &= s_T - s_0 - \dot{s_0}T - \frac{\ddot{s}_0}{2}T^2 \newline 3 a_3 T^2 + 4 a_4 T^3 + 5 a_5 T^4 &= \dot{s}_T - \dot{s}_0 - \ddot{s}_0 T \newline 5 a_3 T + 12 a_4 T^2 + 20 a_5 T^3 &= \ddot{s}_T - \ddot{s}_0 \newline \end{aligned} $$

写成矩阵形式 $$ \begin{aligned} a_3 T^3 +a_4 T^4 +a_5 T^5 &= s_T - s_0 - \dot{s_0}T - \frac{\ddot{s}_0}{2}T^2 \newline 3 a_3 T^2 + 4 a_4 T^3 + 5 a_5 T^4 &= \dot{s}_T - \dot{s}_0 - \ddot{s}_0 T \newline 5 a_3 T + 12 a_4 T^2 + 20 a_5 T^3 &= \ddot{s}_T - \ddot{s}_0 \newline \end{aligned} $$

矩阵形式：

$$ \left[ \begin{matrix} T^3 & T^4 & T^5 \\ 3T^2 & 4T^3 & 5T^4 \\ 6T & 12T^2 & 20 T^3\end{matrix} \right] \left[ \begin{matrix} a_3 \\ a_4 \\ a_5 \end{matrix} \right] = \left[ \begin{matrix} s_T - s_0 - \dot{s_0}T - \frac{\ddot{s}_0}{2}T^2 \\ \dot{s}_T - \dot{s}_0 - \ddot{s}_0 T \\ \ddot{s}_T - \ddot{s}_0 \end{matrix} \right] $$

通过矩阵求逆，可以得到 $[a_3, a_4, a_5]$

Quartic Polynomial

四阶多项式 标准形式： $$ s(t) = a_0 + a_1 t + a_2 t^2 + a_3 t^3 + a_4 t^4 $$

同理 $$ \begin{aligned} a_0 &= s_0 \newline a_1 &= \dot{s}_0 \newline a_2 &= \frac{\ddot{s}_0}{2} \newline \end{aligned} $$ 末端状态： $$ \begin{aligned} \dot{s}_T &= \dot{s}_0 + \ddot{s}_0 T + 3 a_3 T^2 + 4 a_4 T^3 \newline \ddot{s}_T &= \ddot{s}_0 + 5 a_3 T + 12 a_4 T^2 \newline \end{aligned} $$

矩阵形式： $$ \left[ \begin{matrix} 3T^2 & 4T^3 \\ 6T & 12T^2 \end{matrix} \right] \left[ \begin{matrix} a_3 \\ a_4 \end{matrix} \right] = \left[ \begin{matrix} \dot{s}_T - \dot{s}_0 - \ddot{s}_0 T \\ \ddot{s}_T - \ddot{s}_0 \end{matrix} \right] $$ 解得 $[a_3, a_4]$。

测试

frenet

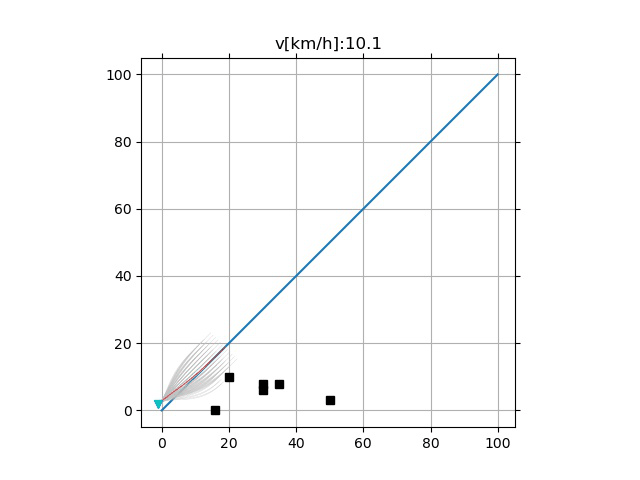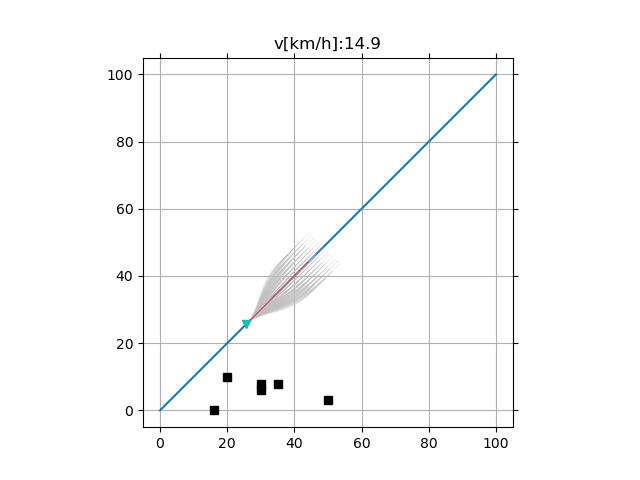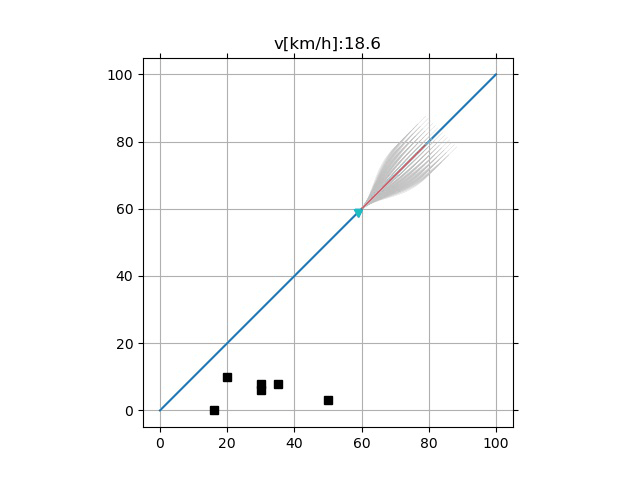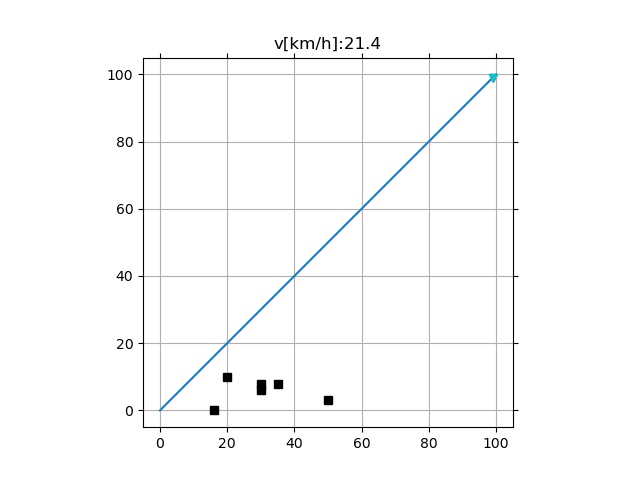
增大 $T_i$ 采样范围

frenet