RT Traj Optimization for Racing

refs: https://github.com/janismac/RacingTrajectoryOptimization

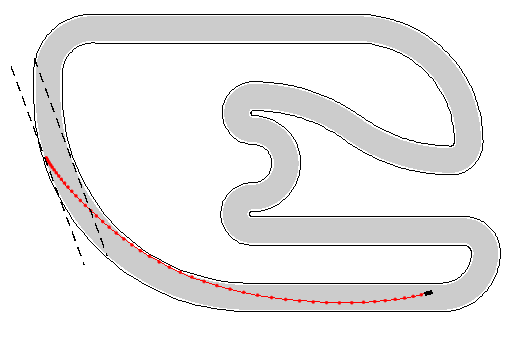
Summary#

以赛道场景，构建了 QP 问题，求解在赛道上可行的轨迹。

• QP 问题要求问题是线性的，且可行域是凸集；文章比较详细的介绍了线性化操作及构建凸集的方法；
• 可借鉴的东西有限，但是作为入门很不错；

术语#

坐标系#

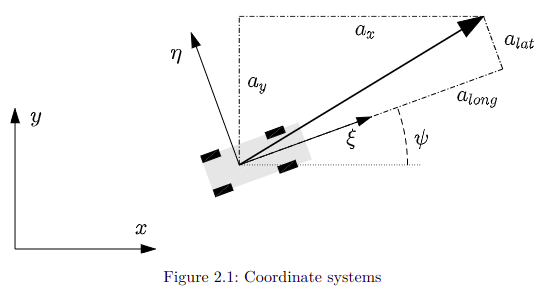
  $x,y$   Global 坐标系
  $\xi, \eta$   Body 坐标系
  $\psi$   Yaw angle
  $[a_{long}, a_{lat}]$   Body 系 加速度
  $u = [a_x, a_y]$   Global 系 加速度

Model#

• 在轨迹规划中，使用质心模型，只考虑质点加速度，能够使轨迹规划成为一个 线性优化 问题；
• 在自动驾驶场景中，汽车的控制通常由油门、方向盘、刹车实现。油门仅提供正向加速度；刹车提供减速度；方向盘改变前轮转向，从而将纵向加速度映射到横向。为方便控制，在 Tracking 过程中，分别实现了横纵向控制器。
• 轨迹优化中，需要考虑加速度限制。尤其是高速行驶过程中的空气影响。

Model Predictive Control#

• 给定被控系统模型和输入，预测未来时刻的系统状态；
• 离散模型按 时间步长 迭代，就可以得到一段离散轨迹；

Race Track Model#

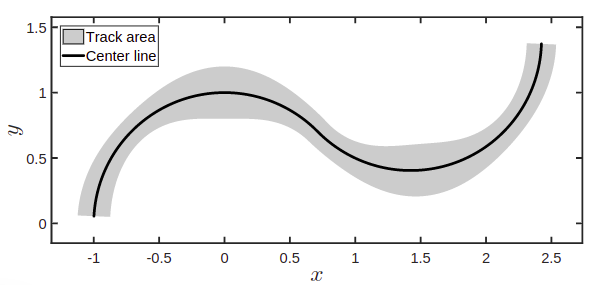
• 赛道模型由中心线 $C$ 和 赛道区域 $T$ 组成；

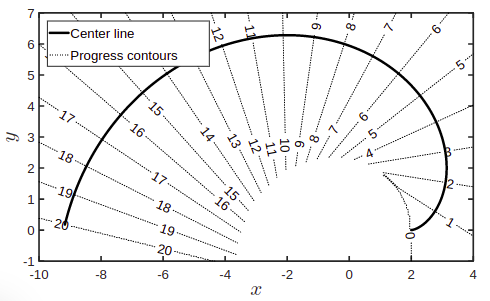
progress function 进度#

• 找到与车辆位置最近的 中心线点，return 从起点到当前 中心线点的弧长；

Approximate Solutions#

• 优化问题通常是非凸的，轨迹优化中最常见的非凸约束是非凸的可行区域。

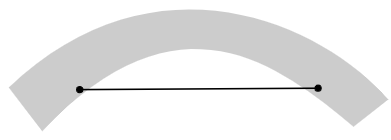
• Sequential Convex Programming
  – Guess 初值
  – 在初值附近构造 QP 问题，求解局部最优解；
  – 逐步迭代，直到解满足条件
  

Trajectory Optimization using Sequential Linearization#

Sequential Linearization#

用于快速找到轨迹规划的近似解。虽然常规的优化算法会一直运行到 满足某个收敛条件 为止，但是在 QP 求解轨迹问题时，通常只执行几次就足以获得一个较好的解。

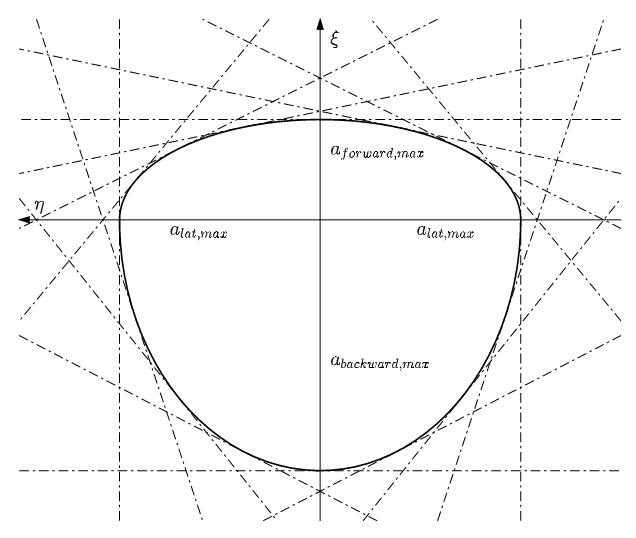
加速度约束#

原始的加速度约束是由两个椭球曲线定义的。但由于 QP 问题要求约束为 线性等式或不等式，所以需要对加速度约束进行线性化。由凸球变为凸多边形：

Race Track Model#

Linear Approximation of the Track Boundaries#

为构造 QP 问题的线性约束，赛道模型需要使用一组线性约束近似。文章中使用 Trajectory Point 处的切线（虚线）近似。

当最终的解与线性化点位置越近时，线性逼近越准确；所以 SL 迭代是渐进稳定的。

在轨迹采样时，通常将道路区域简化为中心线两侧的等宽轨道，$T_{L,j}, T_{R,j}, T_{C,j}$ 表示赛道左侧、右侧和中心线的点； $f_j, n_j$ 表示轨迹点前向、左侧的单位向量：

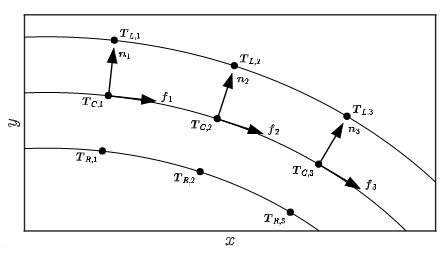
初始化点质量较差、或非线性比较严重时，当前点会出现在轨道约束范围之外。可以引入松弛变量（slack variable）软化约束；将约束条件转化为 Cost，通过优化的梯度保证非严格约束；

Trust Region#

为防止初始点偏差，引起的线性近似误差太大，从而导致不收敛的问题。引入 Trust Region ，将最终结果限制在初值附近，边长为 L 的正方形内

Progress Function#

文章中代价主要表示为 progress function，所以也需要线性化。

Trajectory Optimization Problem#

参考论文 3.3

Trajectory Optimization using Sequential Convex Restriction#

Race Track Model#

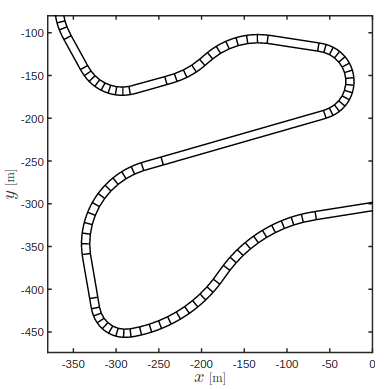
Track Tessellation#

在赛道中心线上采样，并找到左右边界点；相邻的边界点串联得到细分的赛道范围；

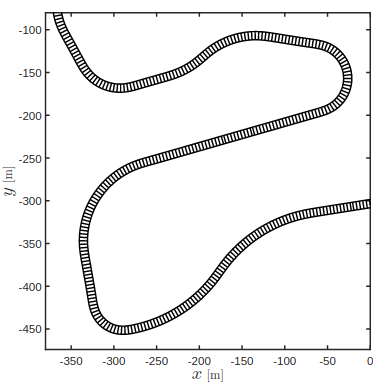
Merging Polygons#

对相邻区域能够组成凸集的，合并；

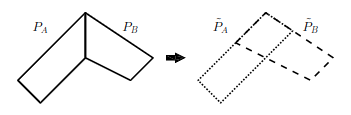
Overlaps#

扩展重叠区域

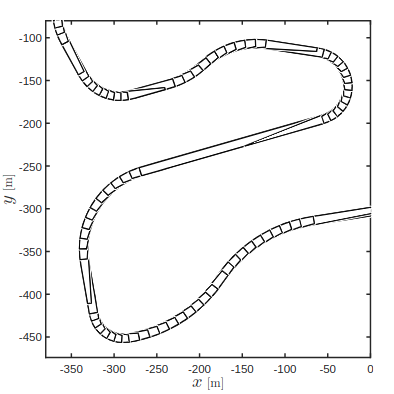
运动过程中，找到的线性化点对应的凸包

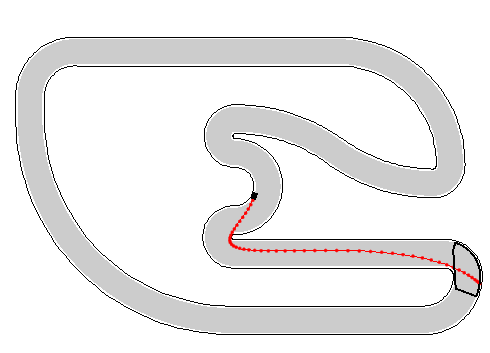
SCR 部分未详细阅读，代码结构相对比较清晰，有缘待续吧。

• Stephen Boyd. Sequential convex programming
• 对于 Sequential Convex Restriction 的可行域图画的比较好： Feasible Path Identification in Optimal Power Flowwith Sequential Convex Restriction
• ROS 中机械臂轨迹库中的轨迹优化： MoveIt - TrajOpt